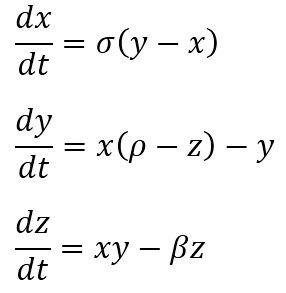آموزش محیط شبیه سازی سیمولینک متلب (Simulink) – شبیه سازی جاذب لورنز (Lorenz Attractor) – قسمت پنجم

سیستم لورنز از دسته معادلات دیفرانسیل معمولی ست که نخستین بار توسط ادوارد لورنز مورد مطالعه قرار گرفت. این معادله دیفرانسیل برای مقادیر پارامتری خاص و شرایط اولیه گوناگون رفتاری آشوبناک از خود نشان می دهد. در واقع جاذب لورنز مجموعه ای از پاسخ های سیستم لورنز می باشد که وقتی ترسیم می گردد مشابه یک پروانه یا شکل عددی 8 مشاهده می شود.

مدل ریاضی معادلات دیفرانسیل معمولی مرتبه سوم سیستم لورنز به صورت زیر تعریف می شود:

که در آن x,y,z متغیرهای سیستم و پارامترهای sigma, ro و beta پارامترهای ثابت سیستم می باشد. برای شبیه سازی سیستم جاذب لورنز پارامترهای سیستم را به صورت زیر در نظر می گیریم:

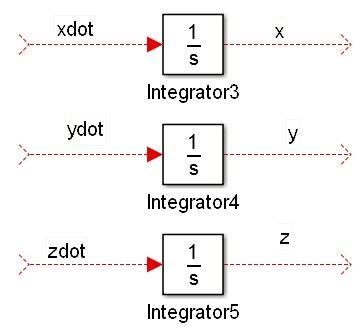
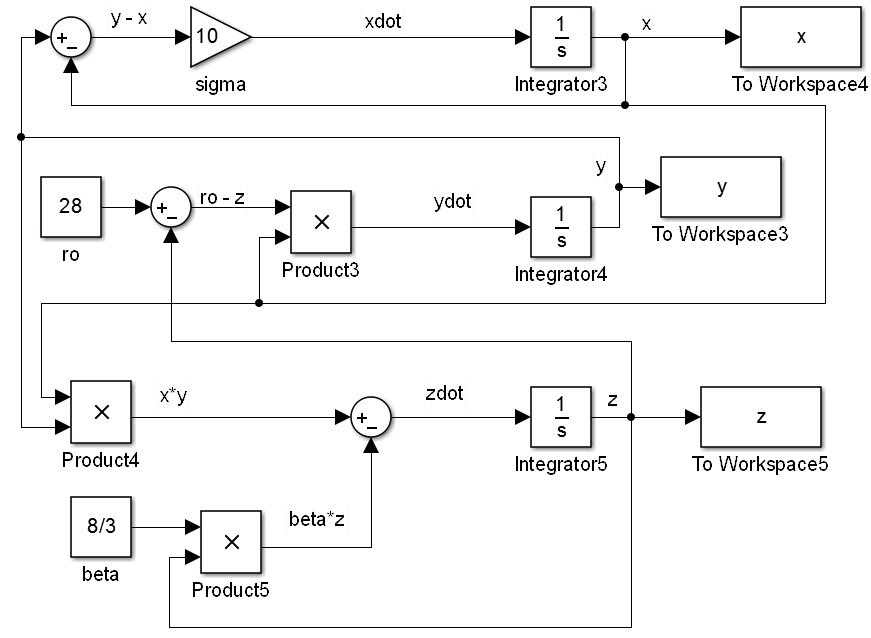
در آغاز شبیه سازی باید یادمان باشد که ما سه معادله دیفرانسیل مرتبه اول داریم. پس به سه انتگرال گیر نیاز داریم. شرایط اولیه را در قسمت initial condition داخل بلوک انتگرال گیرها اعمال می کنیم. برای مثال x0=1, y0=0, z0=0 در نظر می گیریم. داریم:

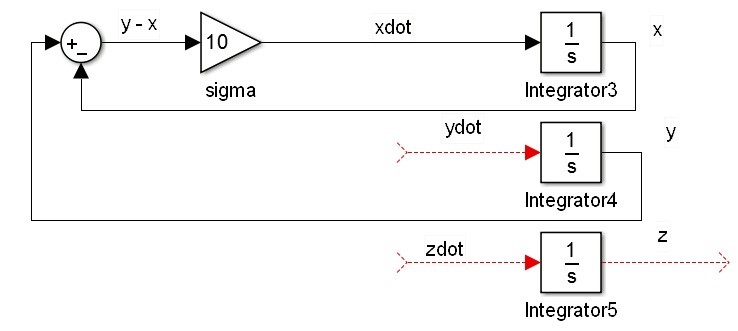
برای مدل سازی معادله dx/dt کافیست تفاضل سیگنال های y و x را در بهره sigma ضرب کنیم. بنابراین از دو بلوک ُSum و Gain استفاده می کنیم. داریم:

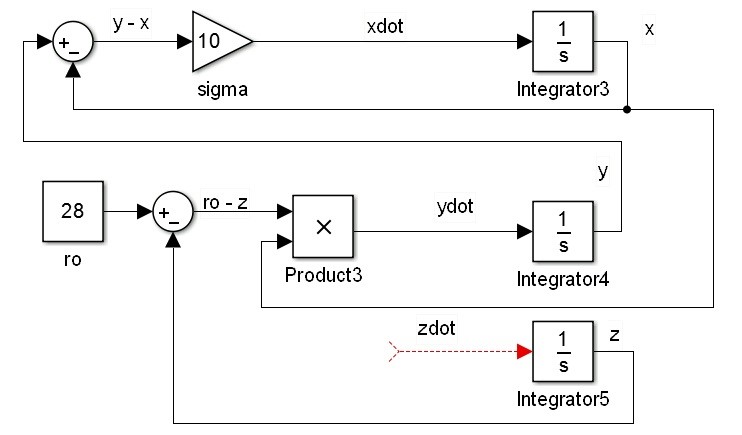
برای مدلسازی معادله dy/dt، کافیست تفاضل عدد ثابت ro و سیگنال z را در سیگنال x ضرب کنیم و حاصل را از سیگنال y کم کنیم. بنابراین در این مرحله از سه بلوک Constant, Product و Sum استفاده می کنیم. داریم:

و در نهایت برای پیاده سازی معادله dz/dt، کافیست حاصلضرب سیگنال های xy را از حاصلضرب پارامتر beta در سیگنال z، کم کنیم. داریم:

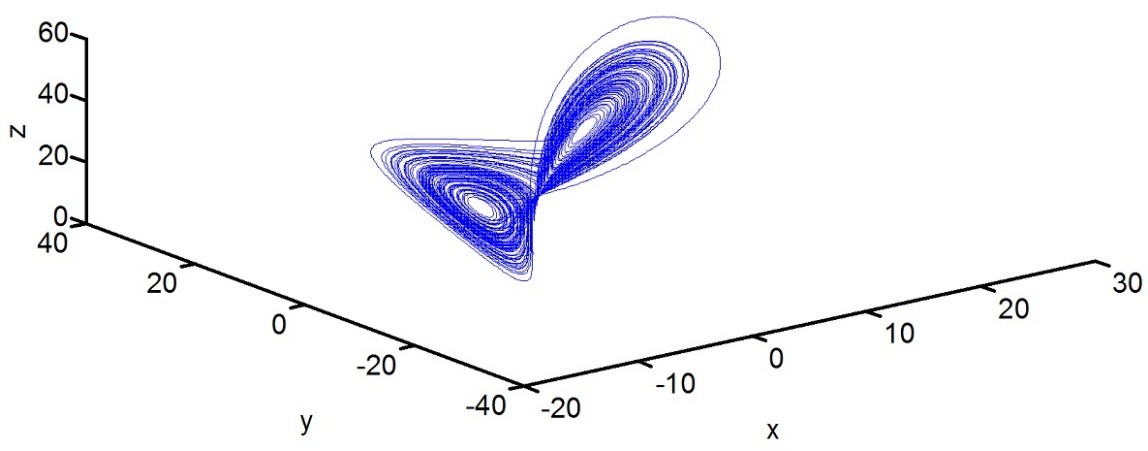
برای ترسیم سه بعدی حالت های سیستم x,y,z در ابتدا با استفاده از بلوک To Workspace و با دو بار کلیک بر روی آن و انتخاب گزینه Array در قسمت Save format متغیرهای x,y,z را در workspace متلب ذخیره می کنیم (در قسمت variable name بلوک To Workspace نام متغیرها را می توانیم تغییر دهیم). حال با استفاده از دستور plot3 به صورت تایپ شده در پنجره Command Window می توانیم رفتاز حالت های سیستم را مشاهده کنیم. داریم:

همانطور که مشاهده می شود وقتی سیستم از حالت های اولیه شروع می کند در لحظاتی حول یک نقطه تعادل ناپایدار سیستم دوران می کند و در لحظاتی حول نقطه تعادل دیگر ناپایدار سیستم دوران صورت می گیرد و این روند ادامه پیدا می کند و اصطلاحا می گویند سیستم رفتاری آشوبناک دارد. در قسمت ششم آموزش سیمولینک، رفتار سیستم لورنز را با کد نویسی (m-file نویسی) نشان می دهیم.