آموزش محیط شبیه سازی سیمولینک متلب (Simulink) – قسمت سوم – حل معادلات دیفرانسیل مرتبه دوم با کد نویسی

معادله دیفرانسیل مرتبه دوم را می توان به فرم کلی زیر در نظر گرفت:

ابتدا معادله دیفرانسیل مرتبه دوم را به سیستم معادلات مرتبه اول تبدیل می کنیم. چون معادله مرتبه دو داریم؛ با تعریف دو متغیر حالت x1 و x2  خواهیم داشت:

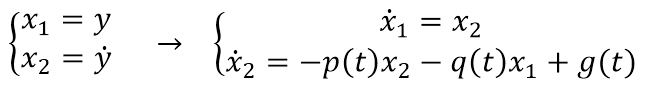
می توانیم دسته معادلات مرتبه اول بدست آمده را به فرم زیر نیز نمایش داد:

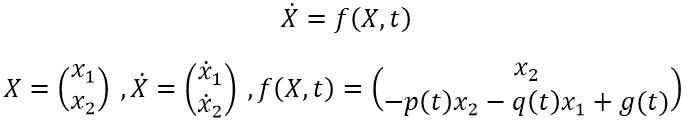
که چون مرتبه معادله دیفرانسیل 2 می باشد برای حل آن به دو شرط اولیه بصورت x1(t0)=y01 و x2(t0)=y02 نیاز داریم. توجه کنید که پاسخ معادله دیفرانسیل یعنی X یک بردار دارای دو المان x1 , x2 می باشد. فرض کنیم می خواهیم پاسخ معادله دیفرانسیل مرتبه دوم زیر را در بازه 0 تا 1 ثانیه و با توجه به شرط اولیه زیر بدست آوریم:

در ابتدا معادله دیفرانسیل بالا را به فرم استاندارد یعنی سیستم معادل معادلات مرتبه اول در می آوریم:

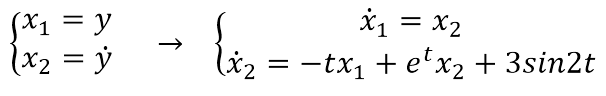
مطابق آموزش قسمت اول، در ویرایشگر (editor) برای m-file نویسی تابع function به صورت زیر کد نویسی می کنیم:

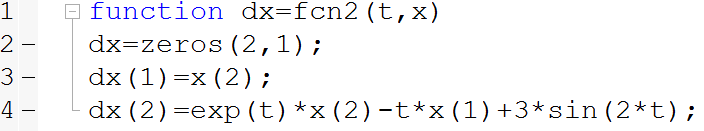
نکته مهم: فراموش نکنیم که در تعریف تابع (function) حتما ابعاد متغیرها در صورتی که برداری هستند به زبان برنامه نویسی متلب شناسانده شود. مثلا متغیر dx یک بردار 1*2 می باشد بنابراین یکی از این روش ها، تعریف یک بردار با المان های صفر توسط دستور zeros می باشد تا به متلب بفهمانیم dx برداری ست. در پایان برنامه نوشته شده را با نام “fcn2” ذخیره می کنیم.

مطابق روش ارایه شده در قسمت اول آموزش، مجددا یک ویرایشگر m-file جدید مثلا به نام mainforfcn2 ایجاد می کنیم. دوباره یادآوری می شود که این کد جدید که می خواهیم بنویسیم، برنامه اصلی می باشد که قرار است توسط آن m-file مربوط به function (برنامه فرعی یا fcn2) فراخوانده شود. پس در ویرایشگر جدید به نام mainforfcn2 دستورات را برای حل معادله با حلگر ode45 به صورت زیر وارد می کنیم:

مثلا فرض کنید می خواهیم هر دو متغیر معادله دیفرانسیل یعنی x1 و x2 را با هم ترسیم کنیم چنانچه به پنجره workspace محیط متلب رفته و متغیر x را مشاهده کنید متوجه می شوید که x دارای دو ستون می باشد که اولی اطلاعات مربوط به متغیر x1 و ستون دوم اطلاعات مربوط به متغیر x2 می باشد. پس ما قرارست که یک بار تمامی اطلاعات ستون اول را بر حسب زمان و نیز اطلاعات ستون دوم را بر حسب زمان ترسیم کنیم که برای این منظور از عملگر کولون “:” استفاده می کنیم. (برای اطلاعات بیشتر به آموزش ماتریس ها در متلب مراجعه کنید – کلیک کنید)

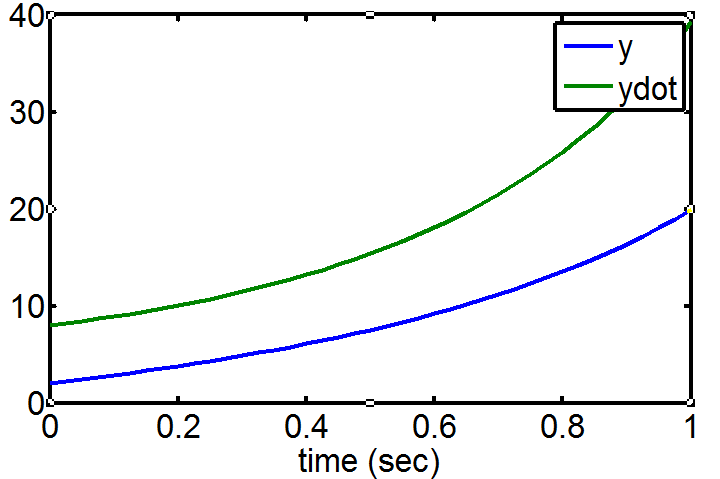
همانطور که مشاهده می شود پاسخ معادله دیفرانسیل (y) و مشتق زمانی آن (ydot) در بازه زمانی 0 تا 1 ثانیه و شرط اولیه 2 برای y و 8 برای ydot ترسیم شده است. در قسمت چهارم آموزش با استفاده از محیط شبیه سازی سیمولینک معادله دیفرانسیل مفروض را حل می کنیم.