آموزش محیط شبیه سازی سیمولینک متلب (Simulink) – قسمت دوم – حل معادلات دیفرانسیل مرتبه اول با کدنویسی

معادله دیفرانسیل مرتبه اول را می توان به فرم کلی زیر در نظر گرفت:

که چون مرتبه معادله دیفرانسیل 1 می باشد برای حل آن به یک شرط اولیه بصورت “y(t0)=y0” نیاز داریم. فرض کنیم می خواهیم پاسخ معادله دیفرانسیل مرتبه اول زیر را در بازه 1 تا 4 ثانیه و با توجه به شرط اولیه زیر بدست آوریم:

در ابتدا معادله دیفرانسیل بالا را به فرم استاندارد در می آوریم:

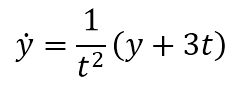
برای تعریف معادله دیفرانسیل بالا در متلب، ابتدا در پنجره “command window” متلب، دستور “edit”را وارد کرده تا ویرایشگر (editor) جدید برای “m-file” نویسی باز گردد. با استفاده از تابع “function” به صورت زیر کد نویسی می کنیم:

مهم: توجه کنید که نام انتخابی برای “function” اختیاری می باشد ( در این مثال”fcn” فرض شده است).  اما توجه شود که زمانی که “m-file” را ذخیره می کنید نام آن با نام “function” حتما باید یکی باشد.

 برای حل عددی معادلات دیفرانسیل روشهای مختلفی وجود دارد که روش “Runge-Kutta” یکی از معروفترین آنهاست. نرم افزار متلب برای حل معادلات دیفرانسیل استفاده از این روش را در قالب حلگر “ode45” توصیه کرده است که به صورت زیر نوشته می شود:

که در آن عبارت داخل گیومه  نام “function” است که در این مثال “fcn” انتخاب شده، “t0” زمان آغازین و “tf” زمان پایانی و “(y(t0” شرط اولیه می باشد. همانطور که مشاهده می شود از دستور “ode45” می توان دو خروجی “t” , “y” را ( سمت چپ عبارت بالا) استخراج نمود. برای حل مثال داده شده مجددا یک ویرایشگر “m-file” جدید مثلا به نام “mainforfcn” ایجاد می کنیم. توجه شود که این کد جدید که می خواهیم بنویسیم، برنامه اصلی می باشد که قرار است توسط آن “m-file” مربوط به “function” (برنامه فرعی) فراخوانده شود. پس در ویرایشگر جدید به نام “mainforfcn” دستورات را به صورت زیر وارد می کنیم:

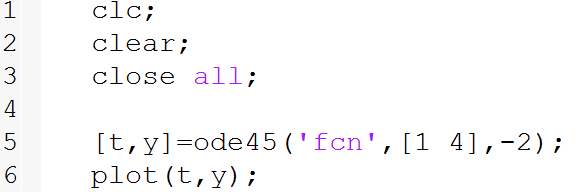
توجه کنید در کد نویسی از دستور “clc” برای پاک کردن “command window”، از دستور “clear” برای پاک کردن “workspace” (جایی که متغیرها ذخیره می شوند) و از دستور “close all” به منظور بستن پلات های از قبل مانده استفاده می شود. برای ترسیم “y” بر حسب زمان می توان از دستور “plot” استفاده کرد که عضو اول محور افق ( در این مثال t یا زمان) و عضو دوم محور عمودی ( در این مثال y)  را نشان می دهد. 

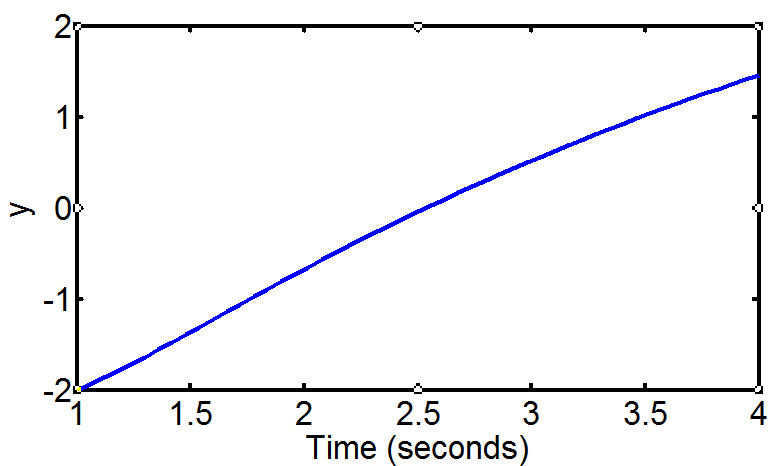
همانطور که مشاهده می شود پاسخ معادله دیفرانسیل در بازه زمانی 1 تا 4 ثانیه و شرط اولیه 2- ترسیم شده است. در قسمت سوم آموزش با استفاده از محیط شبیه سازی سیمولینک با حل معادله دیفرانسیل مرتبه دوم آشنا می شویم.