آموزش برنامه نویسی (کدنویسی) در نرم افزار متلب- (MATLAB) – ماتریس ها و عملیات بر روی آن ها – قسمت چهارم

در این قسمت آموزش عملیات ماتریسی را پی می گیریم. واضح است که عملگرهای ریاضی مانند جمع، ضرب و تفریق در ماتریس ها قابل اعمال است. برای مثال داریم:

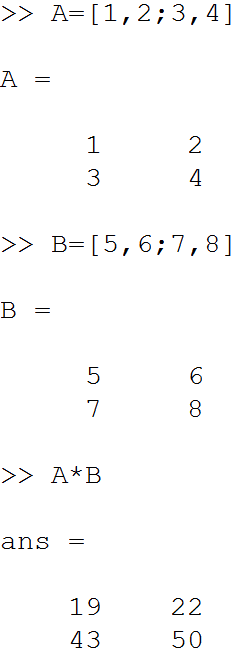
توجه داشته باشید که گاهی اوقات نیاز است که ماتریس ها را عضو به عضو ضرب کنیم. مثلا المان سطر اول و ستون اول ماتریس A در المان سطر اول و ستون اول ماتریس B ضرب شود، المان سطر اول و ستون دوم ماتریس A در المان سطر اول و ستون دوم ماتریس B ضرب شود و به همین ترتیب … برای این منظور اگر قبل از عملگر ضرب، از نقطه استفاده کنیم یعنی “*.” عملگر ضرب تبدیل به ضرب نقطه به نقطه می شود. داریم:

به طور کلی “نقطه” قبل از هر عملگری بیاید آن عملگر را تبدیل به نقطه به نقطه می کند. مثلا فرض کنیم می خواهیم هر عضو از ماتریس A را به توان عضو متناظر آن در ماتریس B برسانیم. داریم

فرض کنیم می خواهیم دو ماتریس A و B را به صورت افقی یا عمودی متصل یا الحاق (concatenate) کنیم. داریم:

یا برای مثال می خواهیم ماتریس A و B را بصورت افقی و در زیر آنها ماتریس B و A- را الحاق کنیم. داریم

اگر خواسته باشیم ماتریس A را 6 بار بصورت افقی در کنار هم و 3 بار بصورت عمودی الحاق کنیم علاوه بر استفاده از روش گفته شده می توانیم از دستور repmat  برای الحاق ماتریس A بصورت افقی و یا عمودی با هر تعداد استفاده کرد. توجه داشته باشید وقتی ابعاد الحاق یک ماتریس بزرگ باشد دستور repmat بسیار راهگشاست. داریم

توجه داشته باشید که یکسری ثابت ها در نرم افزار متلب از قبل ذخیره شده است. به عنوان مثال عدد پی  “pi”. همچنین مفاهیم “بی نهایت” و “تعریف نشده” نیز بر خلاف دیگر زبان های برنامه نویسی در نرم افزار متلب شناخته شده است. مثلا نرم افزار متلب 1/0 را دقیقا به معنای بی نهایت و 0/0 را تعریف نشده در نظر می گیرد. برای مثال اگر در برنامه نویسی نیازمند عددی بسیار بزرگ هستید می توانید از “inf” استفاده کنید. نرم افزار متلب عدد مبهم را به صورت “NaN” که مخفف “Not a Number”  می باشد؛ نمایش می دهد. داریم

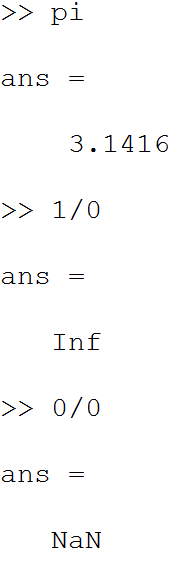
حال فرض کنیم می خواهیم ماتریس A و B را مقایسه کنیم که آیا ماتریس B>A هست یا خیر؟ با استفاده از عملگر قیاس “بزرگتر” یا “<” داریم:

همانطور که مشاهده می شود پاسخ این عملگر قیاس به  صورت منطقی یا (logical) داده شده است یعنی ” True=1″ یا”False=0″  . بدین معنی که عملگر قیاس “بزرگتر”، بزرگی تمام المان های B را با ماتریس A مقایسه می کند و نتیجه می دهد که هر 4 المان ماتریس B بزرگتر از ماتریس A می باشد. حال فرض کنیم می خواهیم ببینیم که آیا عدد “pi” دقیقا برابر 3.14 هست یا خیر؟ برای این کار از عملگر “تساوی” یا “==”  استفاده می کنیم. داریم

پاسخ بصورت منطقی” 0″ یا “خیر” می باشد. دقت کنید که عدد 3.14 رند شده عدد “pi”  می باشد. بنابراین عدد “pi” دقیقا برابر 3.14 نیست. پس به طور کلی به عملگرهای “<” ، “>” ، “==” ، “=<” ، “=>” و … عملگرهای قیاس می گویند که پاسخ آن به صورت داده منطقی”0″ یا “1” ذخیره می شود. در قسمت پنجم آموزش عملیات ماتریسی را ادامه می دهیم.